Variational Quantum Eigensolvers
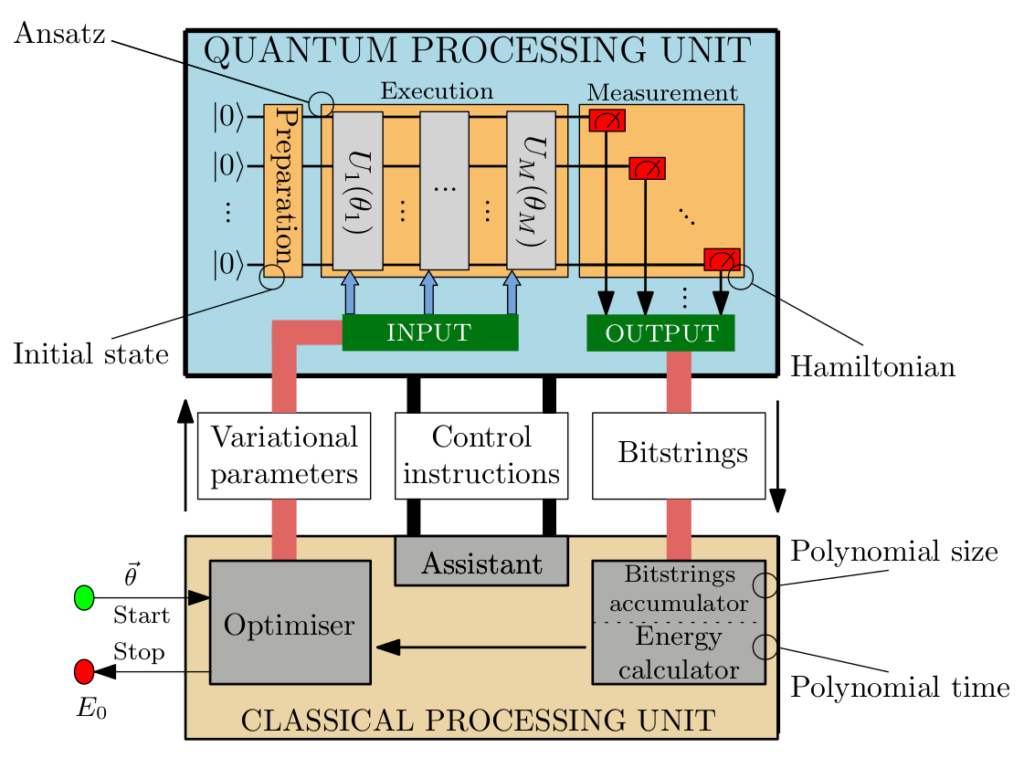
The Variational Quantum Eigensolver (VQE) is a hybrid quantum-classical algorithm designed to solve optimization problems and estimate the ground state energy of quantum systems. By leveraging the strengths of both quantum and classical computing, VQE positions itself as one of the most promising applicable algorithms in the current Noisy Intermediate Scale Quantum (NISQ) era.
In VQE, a quantum computer prepares a parameterized quantum state, known as the ansatz, which is a trial wavefunction dependent on a set of adjustable parameters. This state is measured to estimate the expectation value of the underlying problem Hamiltonian, representing the system’s total energy. The subsequent classical part of the optimization loop is composed of the parameter optimization, i.e. a classical optimizer iteratively updates the parameters to minimize the corresponding energy, ultimately approximating the ground state energy of the system.
The performance of the VQE algorithm highly depends on two factors: the design of the ansatz and the optimization technique used. The latter is a common problem faced in other fields of optimization, e.g. classical machine learning, dealing with local minima and/or barren plateaus. Optimizing the optimization process itself involves selecting suitable classical optimization algorithms and tuning them for the specific problem and hardware at hand. For the ansatz selection, the problem mainly consists of finding an ansatz capturing the ground state, which is already a tough problem on its own, while remaining feasible to compute on the hardware, whether it be a classical simulator or a quantum device.
We focus on improving the ansatz design and developing optimization strategies to enhance VQE’s robustness and accuracy. Those include adaptive ansatz methods, which dynamically adjust used ansätze, and hybrid optimizers combining gradient-based and gradient-free methods, which together form a promising concept tackling the current limitations.
Portfolio Optimisation using Quantum Annealers
The problem in portfolio management lies in the continuous selection of securities within a defined budget. A fundamental goal of portfolio management is to choose a portfolio that strikes a balance between risk and return, in line with predefined risk preferences. The aspects of portfolio management are summarized by Markowitz in a portfolio optimization theory, which forms the basis of the portfolio management considered in our work.
Depending on the additional constraints of this optimization, the problem becomes analytically difficult to solve. It can be formulated as a quadratic optimization problem that can be solved using quantum annealers from D-Wave, which makes it an interesting use case.
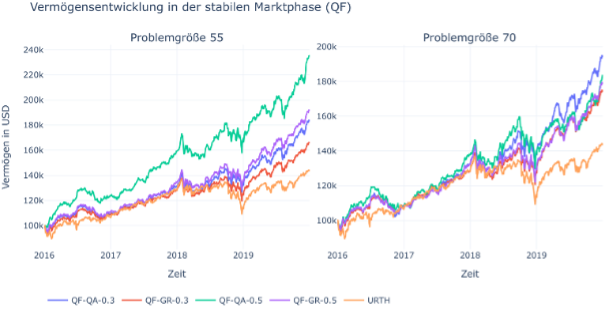
The problem can be described in several ways. Besides different constraints, it is crucial how one maps the continuous character of the underlying problem on the qubits of the quantum annealer. Part of our work is to compare different mapping techniques. After the results are obtained by the quantum annealer, it is possible to enhance the quality of the solution by post-processing. To evaluate the performance of the quantum annealer combined with the pre and post processing steps mentioned above, we build a simulation that runs several optimizations over time and trades assets on the solutions found. Using this approach, it is possible to assess the economic value of the quantum annealer for this task.
Error Mitigation

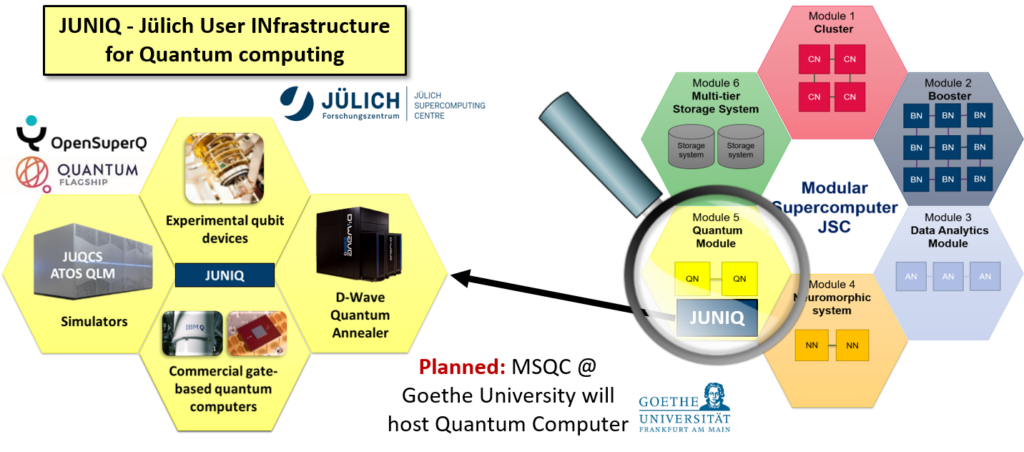
To make quantum computers available to computer scientists, they need to be taken out of the physicists’ labs and integrated into existing high-performance computing centers and infrastructures. We look at various aspects of what needs to be done to make today’s quantum computers easy to use and able to perform useful tasks. One problem that quantum computers suffer from in the current noisy intermediate quantum computing (NISQ) era is the high error rates, that often render the results of computations unusable.
There are error correction methods that combine multiple physical qubits into logical qubits with lower error rates. However, these methods cannot be practically implemented with today’s hardware. An alternative is to post-process the results of the quantum computer calculation with a classical computer in order to mitigate the errors. This involves running calibration programs on the quantum computer and building an error model, which can then be used to mitigate errors in the actual calculation. We are particularly interested in researching scalable error mitigation methods that can be applied to large numbers of qubits.
The figure shows the result of a measurement on real quantum hardware with subsequent error mitigation compared to simulated results. The simulated results, representing the ground truth, are shown in red. The measured results, which deviate from the simulated results due to errors in the calculation, are displayed in blue. The results after error mitigation are shown in purple.
HPC integration of Quantum Computers
HPC Software Toolbox UG4
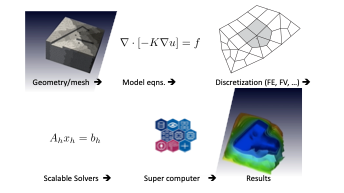
UG4 is an extensive, flexible, cross-platform open source simulation framework for the numerical solution of systems of partial differential equations. Using Finite Element and Finite Volume methods on hybrid, adaptive, unstructured multigrid hierarchies, UG4 allows for the simulation of complex real world models (physical, biological etc.) on massively parallel computer architectures.
UG4 is implemented in the C++ programming language and provides grid management, discretization and (linear as well as non-linear) solver utilities. It is extensible and customizable via its plugin mechanism. The highly scalable MPI based parallelization of UG4 has been shown to scale to hundred thousands of cores. Extension modules allow hybrid programming and computations on GPUs.
Multiscale modeling of diffusion on human stratum corneum
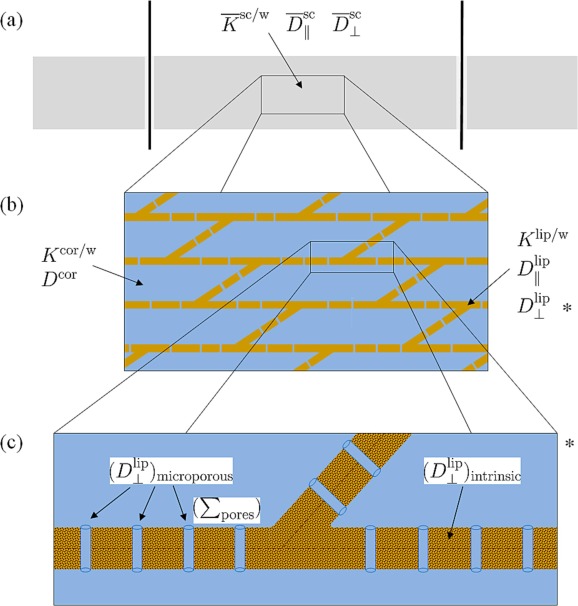
This project enables multiscale mathematical models of drug diffusion through the uppermost layer of the skin, the stratum corneum (SC). It allows for a microscale explanation of the macroscale drug permeability in the SC layer originating from lipid bilayers. The microstructure of SC cells is generally recognized as a recurring pattern of hydrophilic corneocytes embedded in periodic anisotropic lipid bilayers. Therefore, homogenization theory serves as a bridge between the mathematical models.
The simulations require large-scale computations. To that end, multigrid solvers are developed further. This includes, e.g., application of homogenization theory and development of multiscale finite element corrector. This expands the multigrid method for the simulations on large, complicated areas.
Further Reading:
DOI: 10.1016/j.ejpb.2023.01.025
Development of coupling methods across domain boundaries
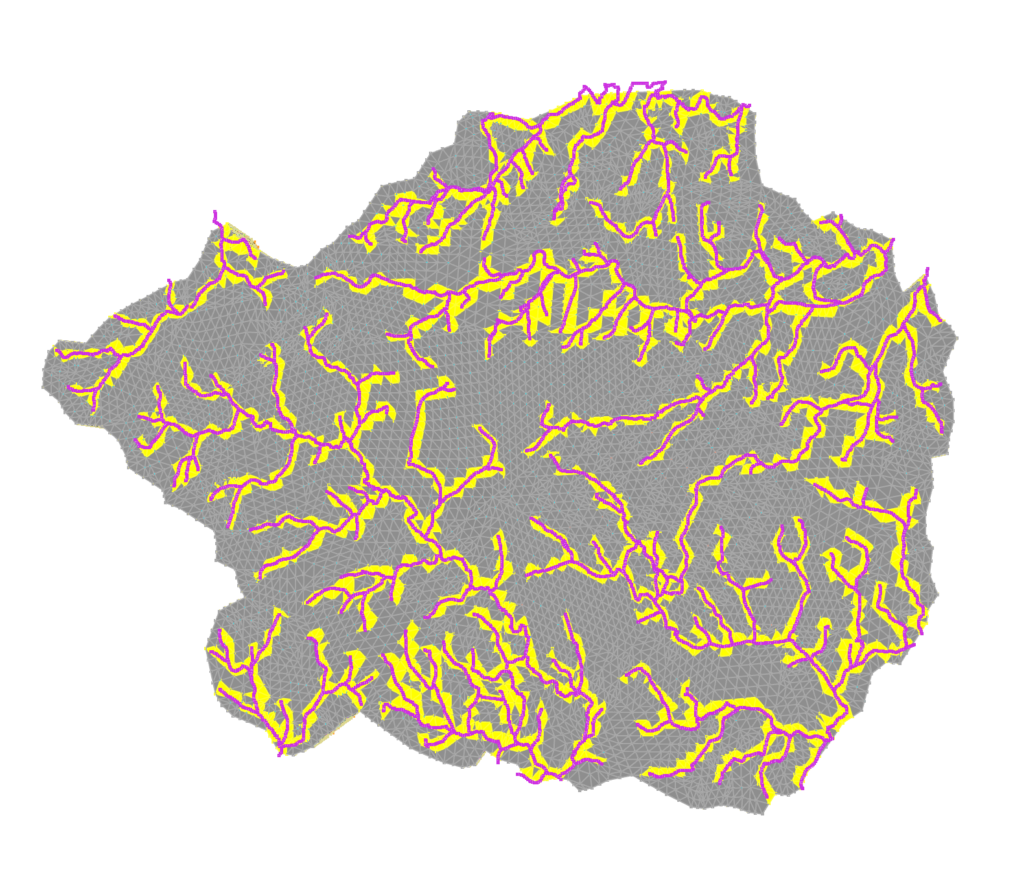
We aim to develop advanced modular coupling methods for solving differential equations across heterogeneous domains. Traditional direct coupling approaches often encounter challenges, particularly when there are significant discrepancies in the required time step sizes between different physical processes.
An illustrative example is the coupling of surface and subsurface flow in hydrological modelling (i.e. exchange fluxes between rivers and groundwater), where surface runoff dynamics operate on much shorter time scales compared to the slower-moving subsurface flow.
By decoupling the simulation of each domain, it is possible to effectively handle variations in temporal scales and physical properties. This is also particularly important for environmental modelling, where points of interest in the simulation domain require additional modelling of the surrounding area to accurately predict future behaviour.
Hierarchical Tucker Format
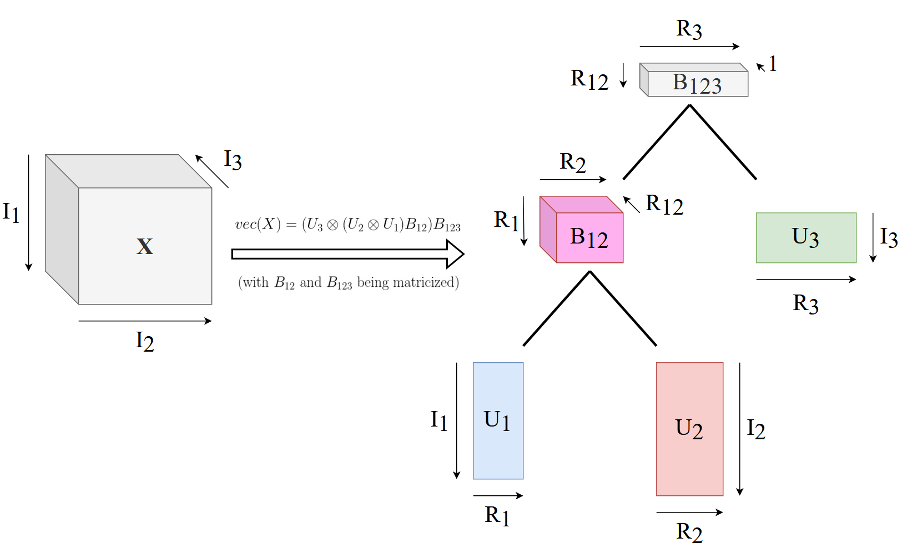
High-dimensional data often pose significant challenges due to the curse of dimensionality, where the computational and storage requirements grow exponentially with the number of dimensions. To address these challenges, the hierarchical Tucker format (HT) offers an efficient tensor decomposition method that mitigates these issues by exploiting low-rank structures.
This project focuses on advancing the HT format for high-dimensional data approximation. Initially applied to model the dynamics of an epidemiological system, the current research aims to integrate classical numerical solution methods with the HT format to enhance computational efficiency and accuracy. A Python library has been developed, utilizing PyTorch as the backend, to support comprehensive algebraic operations within the HT framework.
Additionally, the project explores further applications of the HT format, particularly in scenarios where low-rank properties are present. The ultimate goal is to expand the use of the HT format in scientific computing, providing practical solutions for complex, high-dimensional problems.

